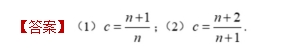2024年全国硕士研究生入学统一考试数学一真题及答案

一 、单项选择题：第1~10小题，每小题5分，共50分。

　1.已知函数，则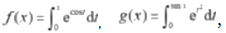

　　A.f(x) 为奇函数， g(x) 为偶函数.

　　B.f(x) 为偶函数， g(x) 为奇函数

　　C.f(x) 与g(x) 均为奇函数.

　　D. f(x) 与g(x) 均为周期函数

　　【答案】C

2. 设P=P(x,y,z),Q=Q(x,y,z) 均为连续函数，2为曲面z=√ 1-x²-y²(x≥0,y≥0)的上侧，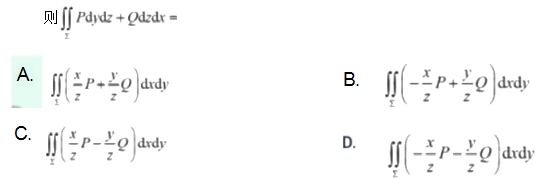

　　【答案】A

　　【答案】A

4. 设函数f(x) 在区间(-1,1)内有定义，则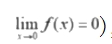

　　【答案】C

　5. 在空间直角坐标系O-n: 中，三张平面π:ax+by+c;:=d,(i=1,2,3)位置关系如图所示，记a,=(a,b,c),B=(a,b,c;,d),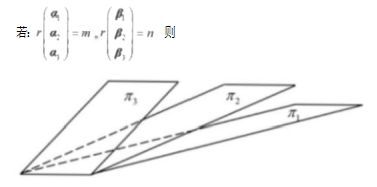

　　A.m=1,n=2 B.m=n=2 C.m=2,n=3 D.m=n=3

　　【答案】B

　　6.识,若g,g,, 转性相关，且其中任意两个向量均线性无关，则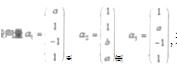

　　A. a=1,b≠-1 B.a=1,b=-1 C. a≠-2,b=2 p.a=-2,b=2.

　　【答案】D

　7. 3阶阵A的联为2,非零向量α满足Aa=0, 任意向量β,使得Fa=0, 且Aβ=β, 则下列结论正确的是

　　A.A的迹为2 B. A的迹为5 C. A 的迹为7 D.A的迹为9

　　【答案】A

　　8. 设随机变量X与Y独立， X 服从N(0,2)的正态分布，Y服从N(-2,2)的正态分布，若P{2X+Y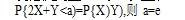    

　　A.-2-√ 10 B.-2+√ 10 C. 2 √6 D.-2+V6

　　【答案】B

　　9. 设随机变量X的概率密度为，在X=x的条件下，Y在区间(x,1) 上服从均匀分布，则 cov(X,Y)=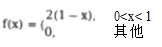

　　10. 设随机变量X,Y相互独立，且均服从参数为入的指数分布，令Z=|X-Y|, 则下列随机变量与Z同分布的是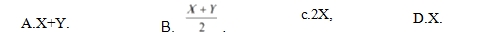

　　【答案】D

　　二 、填空题：第11~16小题，每小题5分，共30分。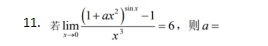

　　【答案】6

　　12.:=f(u,v) 有二阶连续导数，dflug=3du+4dv,y=f(cosx,1+x²),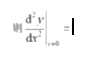

　　【答案】5

　　【答案】α≥0

16. 随机试验每次成功的概率为p, 现进行三次独立重复实验，已知至少成功一次的条件下全部成功的概率为 4/13,则p=

　　【答案】⅔

　　三 、解答题：第17小题10分，第18~22,每小题12分，共70分。

　　17.已知平面区域D={(x,y)| √ 1-y²≤x≤1,-1≤y≤1),计算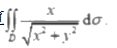

　　【答案】 √2+1n(1+√2)-2

　　18. 设f(x,y)=x²+y³-(x+y)²+3, 曲面z=f(x,y) 在(1,1,1)处的切平面为T,T 与三个坐标面所围有界区域在xoy面的投影为D

　　(1)求T 的方程

　　(2)求f(x,y) 在D 上的最大值和最小值

　　【答案】切平面x+y+z=3;最大值21,最小值为17/27

　　19. 设f(x)二阶可导，f(0)=f^O),UF(x)s1, 证：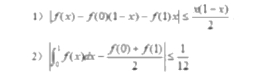

　　【答案】1)泰勒公式

　　2)把1)代入

　20. 已知有向曲线L为球面x²+y²+z²=2x 与平面2x-z-1=0 的交线从二轴正向往二轴负向看去为逆时针方向，计算曲线积分

　　22. 设 总 体 X~U(0,θ),θ 未 知 ， X₁,X₂…X 。 为 简 单 随 机 样 本

　　X(w)=max(Xγ,X₂…X,),T.=cX(o) ·

　　(1)求c 时，使得T 为θ的无偏估计.

　　(2)记h(c)=E(T,-θ)², 求c 使得h(c)取最小值.